Some years ago, a friend of mine introduced our hivemind to a sort of word game or thought experiment. It works thusly:
Every food item is either soup or dumpling. There are no other options. You are not allowed to say “neither” or introduce new categories.
So each ‘player’ works through various examples of food items performing a two-alternative forced choice for each one.
This proceeds smoothly for the examples everyone agrees on. Soup is soup. Cereal in a bowl is not a traditional soup… but sure, you eat it with a spoon, so it’s soupy enough. Similarly, few would disagree that a calzone is a dumpling. Ditto a Boston Cream Doughnut, once you get over the sugar rush.
The fun begins as soon as two ‘players’ disagree about whether some food item is a soup or a dumpling. For me, this happened when rice and curry was introduced. I said this dish was obviously in the soup category. My friend declared that it was clearly a dumpling.
It turns out that for my friend, an important feature of dumplings is the carb-and-something-else combination. For me, wetness seemed to be important for determining soup-ness. Part of the fun my friend derives from this game was the bafflement it provokes in people — especially people who are not inveterate arguers and nitpickers, as my grad school cohort tends to be.

But I somehow found a way to inadvertently turn the tables and irritate my friend! At one point he declared that cheese was soup. I was okay with this. But then he said that a steak was a dumpling. At this point I started to think that there was some quality common to a piece of cheese and a steak that did not feature in a Chinese dumpling (which I implicitly decided must be the canonical dumpling).
So another friend and I began exploring ways to define the soup-dumpling distinction, rather than simply go by gut instinct.
Here is an early attempt:
A dumpling is something that has a clearly defined envelope made of something other than the filling.
So a hunk of cheese, or a piece of steak, can be viewed as a soup! This definition was particularly satisfying to me, because the stipulation of a material difference between the envelope and the filling meant that standard European dumplings — clumps of uniform dough — are not dumplings! Much back and forth ensued (all this was happening during a car ride in Somerville, if I remember correctly), during which I proposed more and more abstract notions of dumplinghood and soupity.

I was particularly proud of a family of operational definitions of dumpling and soup.
If I cut a dumpling in half, I no longer have a dumpling. I have an ex-dumpling. It has ceased to be. So a dumpling is something that displays a kind of integrity or wholeness. You can tell if a dumpling’s envelope has been breached. When this happens, the inside comes in contact with the outside. A soup, on the other hand, does not display this property. If I secretly transfer some soup into another bowl, you may be none the wiser. A mildly recursive definition presents itself:
A dumpling is that which ceases to be a dumpling when divided.
Around this point I was causing serious consternation in the “go with your gut” faction. But things became heated when I decided that dumplingness could actually be viewed along different geometric axes. A swiss roll, for example, could be viewed as dumpling-like along the radial axis, and soup-like along the longitudinal axis.
I was lucky not to be thrown out of the car at this point.
What does this have to do with anything, other than establishing mild insanity in myself and my friends? I’d like to suggest that this game is a window into a variety of cognitive processes, many of which we try to mimic using AI and machine learning.

Definitions are boundaries
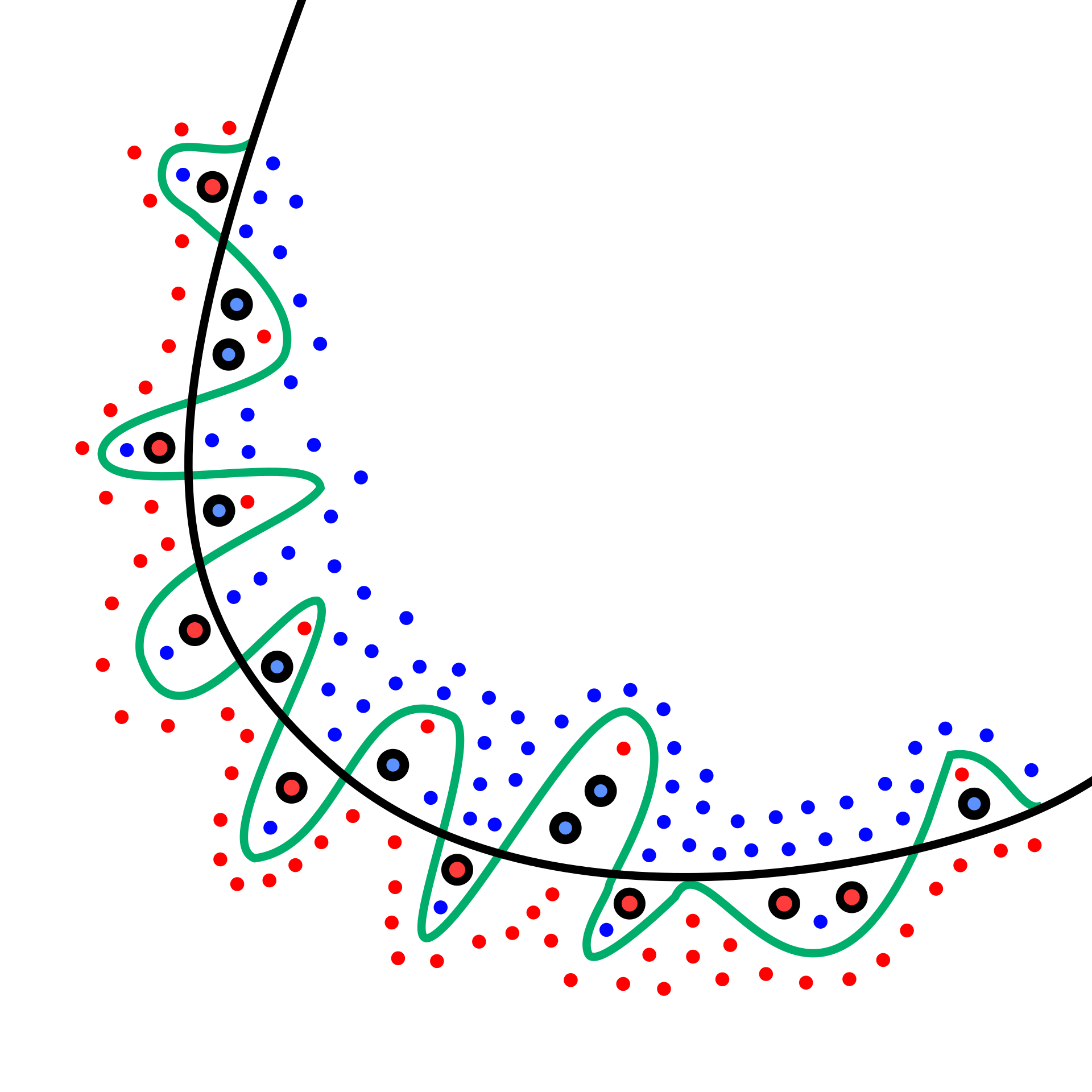
In grad school, our course on memory and machine learning had a very nice semester-long project: we had to perform a pixel classification task using any two ML algorithms. The task is very simple. Given a pixel, the algorithm must categorize it as being inside or outside a pre-specified circle. But the only information that the algorithm can use is a set of labeled examples: pixels labeled as “inside” or “outside” (or white and black, for visualization purposes). This is a toy example of supervised learning. The pixel values (x-y coordinates) are the data points and “inside” vs “outside” are the labels.

What any pixel classification algorithm does is process examples from a training set and distil them into a generalization of some kind. This learned generalization allows the algorithm to classify new data that were not in the training set.
The labeled training set is a case of what philosophers call an extensional definition: it specifies the extension of objects (pixels) falling under the definitions of “inside” and “outside” by simply listing them.
For a potentially infinite number of objects, extensional definitions will not do, since our lists will never be complete. So we seek intensional definitions: ways of specifying the necessary and sufficient conditions for an object to belong to a category.
In the case of labeling pixels, the ideal intensional definition would be the exact mathematical equation for the circle, which might look like x2 + y2 = 1 in a suitable coordinate system.
The nice thing about the exact equation is that it is independent of things like the resolution at which you define pixels. (You do have to decide whether points exactly on the line are inside or outside, but that is a matter of convention.)
So, roughly speaking, every algorithm that performs supervised classification is trying to discover the lines that divide up possibility-space (the space in which objects/pixels live) into non-overlapping zones that correspond to the pre-specified labels or categories. Algorithms differ in how they go about constructing these lines (or “hypersurfaces” when we are talking about higher dimensional data).
When all you have is a bunch of labeled data (i.e., an extensional definition), then you don’t have any intensional “ground truth”. If we are lucky, our AI/ML methods might suggest plausible intensional definitions. But as far as I know, this hasn’t really happened yet in the case of modern AI/ML — it is more true of the history of mathematics, especially since the 19th century. Intuitive definitions of mathematical entities were mined for “labeled data”, which then provided mathematicians with ideas for precise dividing “equations”. In other words, the boundaries between concepts eventually became sharp and infinitely generalizable.
Some of you will see where I am going with this. My attempts at delineating the soup-dumpling boundary are intensional definitions: each one creates an envelope (!) dividing soup-land from dumpling-land in the feature-space of food. But the fun for me was not to be found in settling on some ‘correct’ definition, but instead in the plenitude of mutually inconsistent ways of seeing. The game of definitions is the free play of imagination.
In less playful situations, if there is no previously-existing ground truth (other than gut instinct), we can choose to just work with a definition, resigning ourselves to the absurdities that it may lead to (such as steak being a soup).
But this is not what people typically do (outside of pure mathematics). In domains where conceptual debates are common and mathematical formalisms are few and far between, scholars keep fiddling around with definitions in the hope of avoiding any intuition-violating boundary cases. (Consider attempts to define life or consciousness.) A lesson from ML is that such exercises can be a form of overfitting: we can always cook up complex envelopes that protect our favorite examples from falling on the wrong side of some divide. But this sort of cognitive gerrymandering is fragile, hacky, and not particularly useful.
Obviously not all conceptual problems are analogous to ML classification problems, where explicit tradeoffs and cost functions can guide pragmatic strategies. But… how often do people think of conceptual debates as problems involving costs and tradeoffs? (To say nothing of playfulness, of course.) I suspect that the age-old quest for Truth-with-a-Capital-T, completely stripped of uncertainty and ambiguity, has made people unwilling to consider what they plan to do with the conceptual classifications they seek.
Perhaps we can learn from mathematicians. They do spend a fair amount of time deciding on good intensional definitions. But arguably their greatest successes involve accepting a set of definitions and then patiently exploring their implications, however bizarre. So instead of getting hung up on how a pre-specified problem ought to be framed, they allow the definitions to lead them to undiscovered realms of thought. At the same time, they can flexibly construct new systems — or repurpose old ones — for specific applications (though sometimes it is the physicists who push this… envelope).

A concept is a dumpling
Looping back to our food game, we might be able to use the “topological” notion of a dumpling to highlight some key features of cognition. As we have seen, a definition divides up possibility-space: it creates a “decision boundary” that tells you where a particular category resides. The decision boundary is an envelope separating the objects that are inside the category from those that are outside. So this means that a well-defined concept is a cognitive dumpling!
What do we mean when we say that something is distinct? This means that it can clearly be distinguished from a background. Moreover, when something is distinct, it becomes countable. You can count dumplings by virtue of the fact that they have a discernible boundary. One dumpling plus one dumpling is two dumplings. Metaphysical soup, by contrast, operates using a different algebra: when you combine two soups in a bowl, you get one bigger soup.
Particles are dumplings, fields are soup. Particles are eminently countable. But there is really only one boundless electromagnetic field: we observe undulations and eddies within it.
People who enjoy the feeling of control over things or ideas gravitate towards framing everything in terms of dumplings. Dumplings are easy to manipulate, after all. They come in discrete, portable units. Soupy concepts are much harder to get a handle on, unless we safely restrict the soup to a container of some sort (which, if you think about it, creates a dumpling, since containers are discrete and countable!). Traditional object-based ontologies are dumpling-oriented, whereas process metaphysics posits a gigantic soup. (Ironically, in positing a sharp distinction between traditional objects and fluid processes, process metaphysicians are operating in cognitive dumpling mode.) One can really only delineate a dumpling from the outside, whereas one can be reasonably confident that one is in a soup. The soup-dumpling dichotomy maps onto what Alan Watts called prickles and goo.
Having obeyed the strict soup-vs-dumpling rule, we can step back and ask a different sort of question. Can dumplings becomes soup, and vice versa? If we accumulate a sufficient number of dumplings, they become like the sands of a desert: decidedly soupy. Similarly, if we keep zooming in on a soup, we may find distinctly dumpy constituents eventually.
So when we have the luxury of zooming in and out, or of accumulation and separation, we can see that discreteness and continuity — which the reader has hopefully realized is what we are really talking about here — are two sides of the same coin. Depending on the kinds of questions we might ask, and the kinds of goals we choose, we can adopt two ways of engaging with the underlying mystery, which is neither particulate nor wavy, yet simultaneously both.

For more on the topic of boundaries (and how they relate to Taoism!), see this essay:
Boundaries And Subtleties: The Mysterious Power Of Naming In Human Cognition
The sequel links boundaries with curiosity, via the idea that “interestingness is the first derivative of beauty”:
From Cell Membranes To Computational Aesthetics: On The Importance Of Boundaries In Life And Art
Leave a Reply